Prerequisiti
Nozioni ed abilità precedentemente sviluppate (comandi e procedure
LOGO, concetto di angolo come cambio di direzione).
Obiettivi
- Identificazione di angoli interni ed esterni in una figura geometrica piana
- Creazione di figure geometriche piane attraverso l'impiego di una sequenza di comandi e la successiva verifica della loro accuratezza
- Applicazione del teorema dell'angolo giro per la costruzione di poligoni rfegolari
- Identificazione di alcune proprietà dei poligoni regolari
Fasi del lavoro
-
Disegno di poligoni con carta e penna
-
Verifica della somma degli angoli esterni
-
Costruzione di procedure LOGO per il disegno di poligoni.
-
Disegno di poligoni regolari con l'utizzo del comando "ripeti"
Verifica
Raccolta in una tabella dei dati relativi alle figure piane analizzate.
Disegno e descrizione di un poligono convesso
|
 |
|||||||||||||||||||||||||
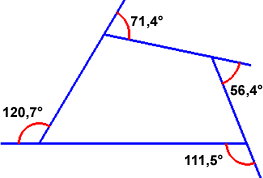
TEOREMA DELL'ANGOLO GIRO Per chiudere il contorno di una figura convessa, la somma delle rotazioni della tartaruga (angoli esterni della figura) deve essere di 360°. Ciò può essere verificato anche empiricamente. Disegnamo un poligono qualsiasi su un pezzo di carta, evidenziamo tutti gli angoli estrni, tagliamoli e appoggiamoli su un foglio in successione, in modo che risultino adiacenti. Possiamo osservare che coprono un'intero angolo giro. |
||||||||||||||||||||||||||
Angolo interno (nero) + angolo esterno (rosso) = 180° 180° x numero lati = S (somma angoli interni + esterni) S - 360° = S' (somma angoli interni del poligono)
|
 |
|||||||||||||||||||||||||
| ||||||||||||||||||||||||||
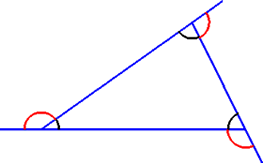
Nel caso di poligoni regolari (angoli e lati congruenti) la tartaruga compie tanti cambiamenti di direzione uguali quanti sono i lati (o gli angooli) del poligono. Quindi l'ampiezza di un angolo esterno è 360°/ n e quella di un angolo interno S'/n |
||||||||||||||||||||||||||