Versione Italiana  Questionnarie
on the 7 strands

Scientific
activities

 Geometrical
activities		 Quadrilaterals Geometrical
transformations

Turtle
geometry

 CABRI files

Drawings

Fractals

Aims

Introducing students to the creation of geometrical figures through a widening of the concept of angle and the use of instruments of measurement

Pre-requirements

Notions and skills previously developed (commands, function keys and the concept of angle as change in direction)

Objectives

  • Identification of exterior an interior angles in plane geometric figures;
  • Creation of a plane geometrical figure employing a set of commands and consequent verification of its accuracy;
  • Application of the round angle theorem (regular figures)
  • Identification of some properties of regular polygons

Working phases

  • Draw polygons on exercise books guided by the teacher
  • Verify the exterior angles sum
  • Draw figures given a set of commands
  • Draw regular geometrical figures using the command “repeat”

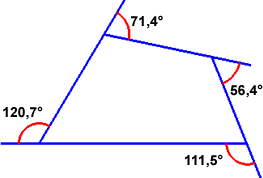
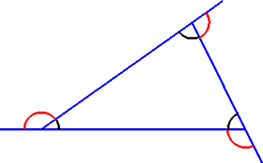
Testing

Gather the data concerning the plane figures and their constitutive elements (sides and angles) in a table.

Activities

Drawing of any kind of polygon (convex)

  • We name is: quadrilateral
  • We use the goniometer to measure the rotation.
  • The rotation is the exterior angle: we check that the exterior angles sum equals 360 degrees.

ROUND ANGLE THEOREM

The turtle, drawing a convex figure, turns 360° all in all.

This may be verified empirically as well: we draw any kind of polygon on a piece of paper, we mark all the exterior angles, we cut them and put them in succession. We may observe that they cover a whole round angle.
The turtle draws the exterior angle, marking the interior angle adjacent to it.

Interior angle (black) + exterior angle (red) = 180°

180° x sides number = S (interior +exterior angles sum)

S - 360° = S' (interior angles sum of the polygon)

 
Interior angles sum of a polygon

n (sides number)

Figure name

S
(Int.+Ext. angle sum)
S'= S - 360°
S'
(Interior angles sum)
3
triangle
180°x3= 540°
540°-360°
180°
4
quadrilateral
180°x4 =720°
720°- 60°
360°
5
pentagon
180°x5 =900°
900°-360°
540°

In the case of regular polygons (congruent angles and sides) the turtle turns 360° in as many identical rotations as the side number (or the angle number) of the polygon.

Thus the exterior angles wideness equals 360°/ n and the interior angles wideness equals S'/n

 
Powered By KMpoint - grscott  
©Copyright 2006 NobelProject.gr