Versione Italiana  Questionnarie
on the 7 strands

Scientific
activities

 Geometrical
activities		 Electricity and batteries Light, colours and vision

Shape and dimensions in living beings

 Studying motion
in real time
An example of how to integrate Mathematics and Science

SHAPE AND DIMENSIONS IN LIVING BEINGS

Does size matter?

  • Why are mammals living in cold regions usually bigger than those living in warmer places? Why do mammals living in the mountains usually have short legs and small ears?
  • Why does a small mammal have a metabolic rate higher than a bigger one?
  • Why does fennec, who lives in Sahara, have big ears?
  • Why are the leaves of plants living in dry regions usually thick?

The ratio of skin surface to mass (or, equivalently, the ratio of surface area to volume) has important consequences for mammals which must maintain a constant body temperature.
The smaller the surface area is, the smaller the heat production is and then the slower the metabolic processes are.

  • When the animals must avoid losses of heat, they have a small skin surface in comparison with their mass.
  • Vice versa, small mammals, having large ratios of surface area to volume, need to produce a great deal of heat in comparison with their size to avoid dying from low body temperature.
  • The amount of food and oxygen they must consume is greater in proportion to their size.
  • The big ears of the fennec allow him to lose a great deal of heat.
    Similar explanation is applicable to the desert plants, that, in order to keep water, must have a small leaf surface.

From a mathematical point of view… Perimeter : Surface area ratio

The rectangles built with rubber bunds on the geoboard have the same perimeter (16 units).
What has the largest area? What the smallest?

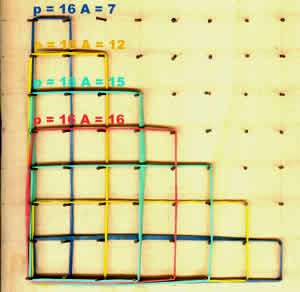Perimeter = 16 units


The square has the largest area (16 u), the “narrowest ” rectangle has the smallest area (7 u).


The unit of length is the horizontal or vertical distance between two consecutive pegs.

The unit of area is one square unit enclosed by four pegs.

Build all the existing rectangles made with 16 squares of 1 cm2. What has the longest perimeter? What the shortest?

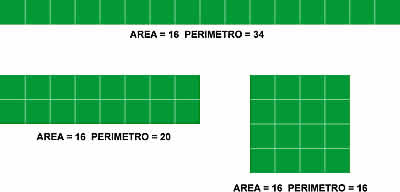Area = 16 units


The square has the shortest perimeter
(16 u), the “narrowest” rectangle has the longest one (34 u).

From a mathematical point of view… Surface area : Volume ratio

With 8 wooden cubes, each representing a volume unit, build all the possible parallelepipeds and measure the surface of each one (assume the face of a cube unit as area unit).
What solid has the largest surface? What solid has the smallest surface?

Volume = 8 units


The solid with smaller surface is the most compact, that is the cube
 (total area = 16 u).

The solid with the largest area is the "longest" parallelepiped
(total area = 34 u)

With the wooden cubes build 3 cubes of different size and determine surface and volume of each one.
How does the ratio surface area: volume vary with the size?

For any given geometric shape (cube, sphere, etc.), smaller objects have a greater surface to volume ratio than larger objects.
As things get bigger their volumes increase rapidly, but their surface areas don't increase as quickly.

CUBE UNIT --> Area/Volume = 6
CUBE MADE WITH 4 UNITS --> Area/Volume =3
CUBE MADE WITH 27 UNITS-->Area/Volume =2

Two empty cardboard parallelepipeds and a cube have the same lateral surface.

In order to compare the volume of the three solids, completely fill them with rice, then weight the rice used for each solid.


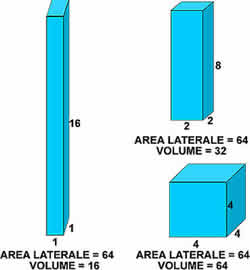Which solid has the larger volume? Which the smallest?

Lateral area = 64 units


The solid with bigger volume is the cube.
The more compact the shape of a solid is, the smaller the ratio Surface/Volume is.

Among the parallelepipeds, the solid “more compact” is the cube, absolutely speaking it is the sphere.
Powered By KMpoint - grscott  
©Copyright 2006 NobelProject.gr